페이지 랭크 계산하는 법 = "반복곱"
1. 각 웹 페이지 $i$의 페이지랭크 점수 $r^{(0)}_i$를 동일하게 $\frac{1}{웹 페이지의 수}$로 초기화
2. 아래 식을 통해 각 웹 페이지의 페이지 랭크 점수 갱신
$$ r_j = \sum_{i\in{N}_{in}(j)} \frac{r_i}{d_{out}(i)}$$
3. 페이지 랭크 점수가 수렴하였으면 종료, 아니면 2번 반복
예시를 들어 살펴보겠습니다.
위 식을 사용하여 계산해보면 어렵지 않게 이해할 수 있습니다!

| 0 | 1 | 2 | 3 | ... | ||
| $r_y$ | 1/3 | 1/3 | 5/12 | 9/24 | ... | 6/15 |
| $r_a$ | 1/3 | 3/6 | 1/3 | 11/24 | ... | 6/15 |
| $r_m$ | 1/3 | 1/6 | 3/12 | 1/6 | ... | 6/15 |
실제로 각 페이지의 랭크는 수렴하는 것을 확인할 수 있습니다.
그렇다면 과연 페이지 랭크는 항상 수렴할까요?
답은 "아니오"입니다!
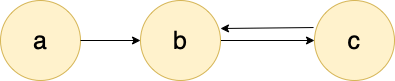
| 0 | 1 | 2 | 3 | ... | |
| $r_a$ | 1/3 | 0 | 0 | 0 | ... |
| $r_b$ | 1/3 | 2/3 | 1/3 | 2/3 | ... |
| $r_c$ | 1/3 | 1/3 | 2/3 | 1/3 | ... |
위와 같은 그래프에서는 페이지랭크가 제대로 수렴하지 않습니다!
이렇게 수렴하지 않는 문제가 발생하는 이유는 바로 "스파이더 트랩(Spider Trap)"때문입니다.
스파이더 트랩이란?
들어오는 간선은 있지만 나가는 간선은 없는 정점 집합
그렇다면 반복곱은 합리적인 점수로 수렴하는 것을 보장할 수 있을까요?
이것도 "아니오"입니다.

| 0 | 1 | 2 | 3 | ... | |
| $r_a$ | 1/2 | 0 | 0 | 0 | ... |
| $r_b$ | 1/2 | 1/2 | 0 | 0 | ... |
위 예시는 "막다른 정점(Dead End)"에 대한 문제입니다.
막다른 정점(Dead End)란?
들어오는 간선은 있지만 나가는 간선이 없는 경우
이런 문제를 해결하기 위해서는 순간이동 (Teleport)라는 개념의 도입이 필요합니다.
순간이동(Teleport)란?
1) 현재 웹 페이지가 막다른 정점(하이퍼 링크가 없다면) 임의의 웹 페이지로 순간이동
2) 현재 웹 페이지에 하이퍼링크가 있다면
a. $\alpha$의 확률 : 하이퍼링크 중 하나 균일한 확률로 선택
b. $(1-\alpha)$의 확률 : 임의의 웹 페이지로 순간이동
이로 인해 스파이더 트랩이나 막다른 정점에 갇히는 경우에서 벗어날 수 있게 됩니다!
보통 $\alpha$의 값은 0.8을 사용한다고 합니다.
순간이동을 사용하게 되면 페이지랭크를 구하는 수식은 아래와 같이 변형됩니다.
$$ r_j = \sum_{i\in{N}_{in}(j)}\left( \alpha \frac{r_i}{d_{out}(i)} \right) + (1-\alpha) \frac{1}{|V|}$$
* $|V|$ 는 전체 웹 페이지 수
본 글은 부스트코스 "그래프와 추천 시스템" 강의를 듣고 공부하며 정리 및 재구성한 글입니다.
그래프와 추천 시스템
부스트코스 무료 강의
www.boostcourse.org
'DL & ML > Graph' 카테고리의 다른 글
| [DGL] ndata, edata, srcdata, dstdata란? (0) | 2022.02.04 |
|---|---|
| [DGL] Graph와 Heterogeneous Graph의 차이 (0) | 2022.02.04 |
| [그래프와 추천 시스템] 페이지 랭크 (0) | 2022.01.28 |
| [그래프와 추천 시스템] 그래프 패턴 - 다양한 그래프 패턴 (0) | 2022.01.28 |
| [그래프와 추천 시스템] 그래프 패턴 - 실제 그래프와 랜덤 그래프 (0) | 2022.01.28 |


