본 글은 논문을 읽고 공부를 하는 과정에서 이해한 바를 번역 / 설명 해둔 글입니다.
혹시 동일 논문을 읽는 다른 분들께 도움이 되었으면 하여 정리해두나 잘못된 부분이나 부족한 부분이 있을 수 있습니다.
따라서 잘못된 부분 / 궁금한 부분이 있으면 언제든지 댓글 환영합니다.😄
최근 heterogeneous graph를 다루는 방법에 대해서 연구하면서 찾게 된 논문이다.
작년 하반기에 나온 매우 따끈따끈한 논문!
한 번 정리하면서 읽어보려 한다.
heterogeneous graph와 homogeneous graph의 차이가 궁금하다면 이 글을 참고하길 바랍니다!
HMSG: Heterogeneous Graph Neural Network based on Metapath Subgraph Learning
Many real-world data can be represented as heterogeneous graphs with different types of nodes and connections. Heterogeneous graph neural network model aims to embed nodes or subgraphs into low-dimensional vector space for various downstream tasks such as
arxiv.org
0. Abstract
Real-world 데이터는 다양한 타입의 노드와 연결로 이루어진 heterogeneous graphs로 표현할 수 있습니다.
Heterogeneous graph neural network 모델은 주로 노드를 임베딩하거나 서브 그래프를 저차원으로 표현하여 node classification하거나 link prediction 등을 하는 데에 주로 사용이 됩니다.
비록 여러 모델들이 최근에 제안되었으나 주로 동일한 타입의 이웃으로부터 정보를 취합하거나 heterogeneous의 neighbors를 homogeneous에서와 동일한 방법으로 식별을 합니다.
실제로 dgl 라이브러리에서 Heterogeneous Graph의 convolution layer를 살펴보면 각 관계 마다 각각의 이웃으로부터 취합하는 형식으로 heterogeneous를 각 관계 / 노드 별 서로 다른 homogeneous graph와 유사하게 다루고 있다는 것을 확인할 수 있습니다.
3.3 Heterogeneous GraphConv 모듈 — DGL 0.9 documentation
3.3 Heterogeneous GraphConv 모듈 (English Version) HeteroGraphConv 는 heterogeneous 그래프들에 DGL NN 모듈을 적용하기 위한 모듈 수준의 인캡슐레이션이다. 메시지 전달 API multi_update_all() 와 같은 로직으로 구현되
docs.dgl.ai
본 논문에서는 새로운 heterogeneous graph neural network modeldls HMSG를 제안합니다.
homogeneous와 heterogeneous graph 모두 이웃으로부터 더 구조적이고 의미적인 정보를 이끌어내는 것이 이 모델의 목표입니다.
본 논문에서 제안하는 방식은,
1. heterogeneous graph를 여러개의 metapath-based homogeneous / heterogeneous subgraph로 분해 (각 서브그래프는 특정 의미와 구조 정보로 연관되어있음)
2. 각 서브그래프에 독립적으로 message aggregation methods 적용
이를 통해 정보는 보다 효율적인 방법으로 학습이 가능해집니다.
이때 노드 type 별 attributes 변환을 통해 서로 다른 타입의 노드 간에도 message aggregation이 될 수 있게 해줍니다.
3. 완벽한 representation을 얻기 위해 각 서브그래프의 정보를 모두 결합
1. Introduction
위에서 말했듯, 많은 real-world 데이터는 그래프 / 네트워크 구조로 표현했을 때 관계와 다양한 목적의 추상적인 표현을 더 잘 나타낼 수가 있습니다.
예를 들면 social networks, traffic networks, protein molecular 구조, 추천 시스템 등이 대표적인 예라고 할 수 있죠.
그러나 non-Euclidean data(그래프)에 현재 Euclidean data에 주로 사용되는 CNN과 RNN 같은 딥러닝 모델은 바로 적용할 수가 없습니다.
그러니 graph data에 적절한 새로운 딥러닝 모델을 설계하는 것이 필요한 것이죠.
그래서 지난 10년 동안, 많은 graph representation 학습 방법이 제안되었습니다.
Random-walk를 기반으로 한 DeepWalk 방식도 있었고,
random walk를 사용하여 그래프에서의 node sequences를 샘플링 한 node2vec이 있었고,
이를 skip-gram model에 적용하여 각 노드의 저차원 vector 표현을 얻는 모델도 있었습니다.
그 외에도 그래프 데이터에서 RNN을 사용하는 모델도 있었구요.
CNN의 강력한 feature 추출 능력때문에 많은 graph convolutional neural networks 또한 매우 큰 성공을 거두었습니다.
ChebNet과 GCN은 푸리에 변환을 사용하여 그래프 데이터에 convolution을 적용하였습니다.
GraphSAGE나 GAT와 같이 노드의 이웃들 정보를 직접적으로 결합하여 좋은 일반화 성능과 안정성을 보여주는 모델도 있었습니다.
이렇게 많은 graph embedding 관련 논문이 좋은 성능을 보여주었음에도!
이러한 대부분의 모델들은 homogeneous graph를 다루고 있다는 한계점이 있습니다.
그러나 현실의 그래프는 대체로 여러 종류의 노드와 엣지를 가지고 있는 heterogeneous라는 것이죠.
예를 들면, scholar graph에는 authors와 papers가 있을 것이고, 추천 시스템에서는 사용자와 아이템이 있겠죠.
따라서 최근에 이러한 heterogeneous graphs 표현 학습에 많은 연구 노력을 기울이는 추세입니다.
Motivations.
대부분의 heterogeneous graph에 대한 연구는 metapath를 기반으로 합니다.
metapath란 노드 타입과 엣지 타입의 순서를 정의하는 것으로 그래프의 특정한 의미 정보를 캡쳐하는데에 주로 사용이 됩니다.
예를 들어, 저자, 논문, 학회를 표현하는 간단한 co-author graph가 있다고 가정해봅시다. (그림 (a))
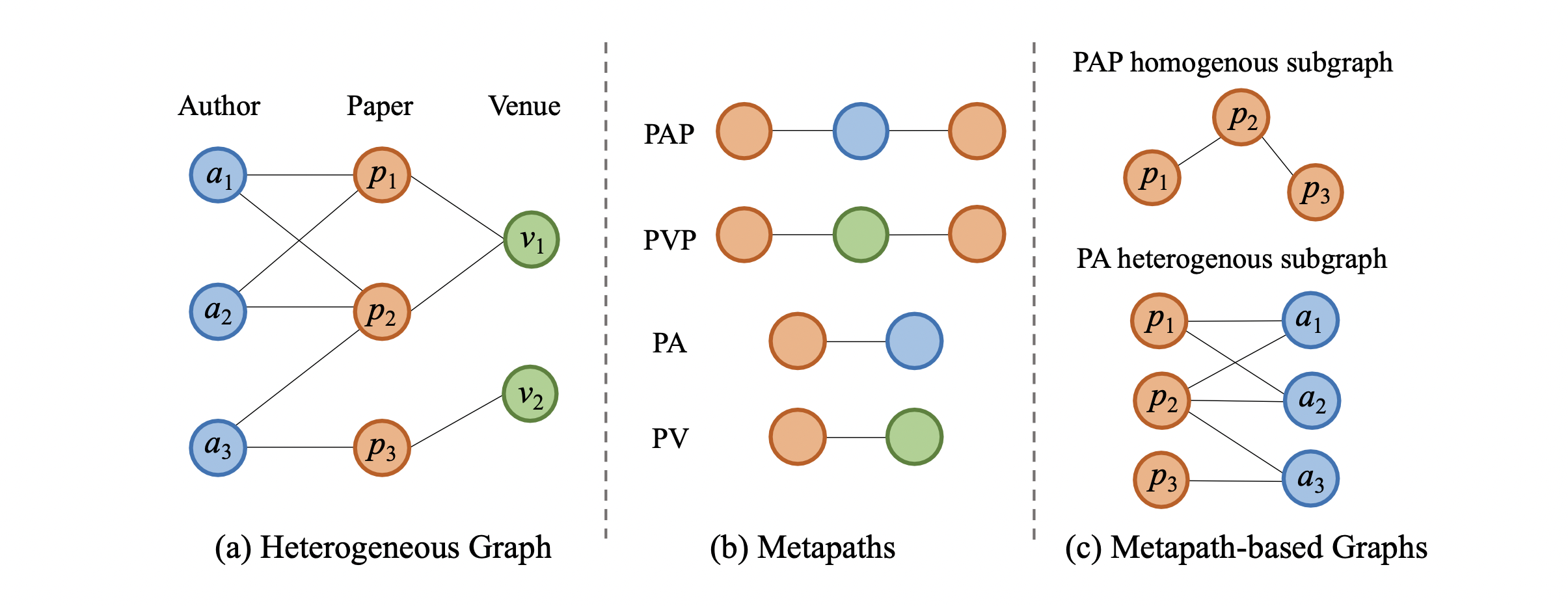
이를 metapath로 표현한 것이 그림 (b)입니다.
PAP는 논문 - 저자 -논문, PVP는 논문 - 학회 - 논문등으로 (a)의 관계성을 표현한 것이죠.
예를 들면 PAP는 p1 -> a1 -> p2 정도가 될 수 있겠네요.
이러한 metapath 방법을 베이스로 metapath2vec, HIN2vec, HERec등의 heterogeneous graph 구조를 저차원의 벡터로 임베딩하는 여러 방법이 제안되었습니다.
HetGNN, HAN, MAGNN 같은 모델에서는 heterogeneous graph 내의 노드의 속성을 통합하고 attention을 사용하여 여러 metapaths 또는 이웃들의 임베딩을 aggregate하는 방법을 제안했습니다.
그러나 이러한 heterogeneous graph 모델들은 다음과 같은 두가지 한계점이 있습니다.
1. metapath에 의해 연결된 homogeneous neighbors로부터의 정보만을 수집하고 heterogeneous 이웃들의 풍부한 구조와 정보는 그냥 버려버립니다.
2. 몇 연구들은 homogeneous와 heterogeneous 이웃들 모두 정보를 수집하나 서로 다른 이웃들을 동일한 방식으로 다룹니다.
그 결과 중요한 정보를 잃게 되고 불만족스러운 성능이 나타내게 되는 것이죠.
위 Figure1에서 그림 (c)을 보면 PAP 타입의 metapath로 homogeneous subgraph를 구성한 예제가 있습니다.
homogeneous subgraph로 만든 것이므로 paper nodes인 p12, p2, p3로만 이루어져있죠. (A 노드는 P노드를 연결 짓게 해주는 일종의 다리 역할입니다.)
만약 노드 p2를 기준으로 homogeneous neighbors(p1, p2)의 정보만 취합하게 된다면 이들을 연결해주는데 기여한 heterogeneous 이웃들(a1, a2, a3)의 정보는 무시 될 것입니다.
그러므로 단순히 homogeneous graph만을 고려하는 것은 기존 그래프의 유용한 상호작용 정보를 잃게 되는 것입니다.
이러한 상호 관계성은 link prediction과 같은 tasks에서 특히 매우 중요할 수 있음에도 불구하고 무시되는 것이죠.
게다가 타겟 노드와 다른 타입의 이웃 노드 사이에는 서로 다른 interactive relationships가 존재합니다.
이러한 관계는 서로 다른 의미를 가지고 있기 때문에 정보 손실을 피하기 위해 별도로 고려해주어야 합니다.
즉, 서로 다른 타입의 노드는 서로 다른 속성을 가지고 있음을 언급해줄 필요가 있는 것이죠.
예를 들어, 추천 시스템에서는 사용자 노드는 일반적으로 나이, 성별, 취미와 같은 속성을 가지고 있는 반면 아이템 노드는 가격, text 설명, 이미지 등의 속성을 가지고 있을 것입니다.
이렇게 서로 다른 속성을 서로 다른 타입의 노드에게 바로 전송할 수 없기 때문에 먼저 변환 과정을 거쳐야 합니다.
본 논문 저자가 아는 한 이러한 두가지 측면을 모두 동시에 고려한 연구는 기존에 없었다고 합니다.
이를 바탕으로 본 논문에서는 새로운 heterogeneous graph representation 학습 모델인 HMSG(Heterogeneous graph neural network based on Metapath SubGraph learning)을 제안합니다.
이 모델은 의미, 구조, 속성 정보를 homogeneous와 heterogeneous의 이웃으로부터 모두 캡쳐할 수 있는 모델입니다.
이를 위해서 먼저 서로 다른 타입의 노드 속성을 동일한 latent space로 투영하기 위해 특정 타입의 속성을 변환하여 서로 다른 타입의 노드끼리 message를 전송할 수 있게 만들어줍니다.
그 후, 더욱 차별적으로 학습하기 위해 기존 heterogeneous graph의 metapath로부터 추출한 여러개의 homogeneous / heterogeneous subgraph를 생성합니다.
이 과정을 통해 기존의 복잡한 구조와 의미적 정보를 보다 효율적으로 학습할 수 있게 됩니다.
homogeneous와 heterogeneous subgraphs를 독립적으로 학습함으로써 HMSG는 homogeneous 이웃들로부터 정보를 수집할 뿐만 아니라 heterogeneous의 이웃들로부터 속성과 구조적인 정보를 얻을 수 있습니다.
이때 각각의 서브그래프에서 노드의 representation을 얻기 위해 서로 다른 aggregation 방법을 사용할 수 있습니다. (그래프 타입에 따라)
마지막으로 attention-based aggregation을 수행하여 중요도에 따라 다른 서브그래프들로부터 정보를 combine하고 최종적인 노드 representation을 생성합니다.
결론적으로 말하자면 본 논문의 된 내용은 다음과 같습니다.
- HMSG라는 metapath-based heterogeneous graph neural network 모델을 제안
- 이는 homogeneous와 heterogeneous 이웃들 모두로부터 구조적, 의미적, 속성 정보를 모두 캡쳐해낼 수 있음
- heterogeneous graph representation learning task를 여러 Metapath 기반 subgraph learning tasks로 분해하여, 기존의 복잡한 구조적, 의미적 정보를 더 효율적으로 학습할 수 있도록 함
- node classification, node clustering, link prediction을 여러 데이터셋으로 실험해본 결과 최고의 성능 달성!
2. Related Work
2.1 Graph Neural Networks
GNN의 목적 : 그래프 표현을 학습하기 위해 딥러닝 모델을 적용한 것!
저차원의 vector space로 그래프를 맵핑하여 node classification, link prediction, 추천 등에 사용합니다.
최근에는 convolutional 신경망을 graph data에 적용하는 것이 굉장히 핫한 주제입니다.
관련 연구들은 크게 두 가지 카테고리로 나눌 수 있습니다.
1) spectral-based 방법
2) spatial-based 방법
spectral-based 방법의 메인 아이디어는 Fourier domain에서 convolution 연산을 수행하는 것입니다.
spectral-based 방법은 연산을 수행하기 위해서 전체 그래프가 다 input으로 들어가야 하기 때문에 scalability / stability 문제가 심각합니다.
spatial-based 방법은 각 노드의 이웃들로부터 정보를 직접적으로 수집하는 방법입니다.
이들과 관련된 여러 논문들이 존재하지만, heterogeneous graph에 직접적으로 적용할 수 있는 방법은 없습니다.
2.2 Heterogeneous Graph Embedding
Heterogeneous graph embedding의 목적 : heterogeneous graph를 저차원의 vector space로 임베딩하는 것!
<생략>
3. Preliminaries and Problem Statement
다음은 본 논문에서 사용되는 정의입니다.
Definition 1. Heterogeneous Graph
앞에서도 충분히 설명되긴 했지만!
Heterogeneous graph는 node type mapping function $ V -> A $와 edge type mapping function $ E -> R $이 존재하는 $G = (V, E) $인 그래프가 있을 때, $|A| + |R| > 2 $를 만족하는 그래프입니다.
즉, 노드 또는 엣지 타입이 한가지 이상을 의미하는 것이죠!
예를 들어, 위에서 설명했던 저자, 논문, 학회 그래프가 바로 여러 개의 노드 타입이 존재하는 그래프입니다.
Definition 2. Metapath
metapath P는 $ A_1 -> A_2 -> ... -> A_{l+1} $ 의 형태로 표현하는 것을 의미합니다.
만약 metapath $P$와 reverse $P^{-1}$가 동일하다면 $P$는 symmetric하다고 말할 수 있습니다.
예를 들어 Figure 1(b)에서 4가지 PAP, PVP, PA, PV metapath가 있습니다.
서로 다른 metapaths는 서로 다른 의미를 가지고 있습니다.
Definition 3. Metapath-based Neighbor
heterogeneous graph의 node v와 metapath P가 주어졌을 때 metapath-based neighbors $N_v^P$는 metapath P를 통해 노드 v를 연결짓는 노드들의 집합을 의미합니다.
예를 들어, Figure1에서 metapath PAP를 보면, p1의 metapath-based neighbors는 p1, p2, a1, a2가 있습니다.
본 논문에서는 metapath의 starting node를 target node로 지정합니다.
Definition 4. Metapath-based Subgraph
heterogeneous graph의 metapath P가 주어졌을 때, metapath-based subgraph $G^P$는 그래프 $G$의 metapath$P$를 기반으로 모든 이웃 쌍으로 구성 된 그래프입니다.
만약 $P$의 처음과 끝이 동일한 노드 타입이라면 $G^P$는 homogeneous subgraph일 것이고, 그렇지 않다면 heterogeneous subgraph일 것입니다.
예를 들어, Figure1 (c)를 보면 두가지 metapath-based subgraph가 있습니다.
1) metapath PAP에 의해 생성된 homogeneous subgraph
2) metapath PA에 의해 생성된 heterogeneous bipartite subgraph
Heterogeneous Graph Representation Learning Problem.
heterogeneous graph가 주어졌을 때 풍부한 구조적, 의미적, 속성 정보를 가지고 있는 d차원의 node representation을 학습하는 것입니다.
아래는 본 논문에서 쓰이는 여러 수식 기호입니다.

4. Methodology
자, 이제 HMSG에 대해서 자세히 알아보도록 합시다.
HMSG는 크게 4가지 파트로 이루어져있습니다.
(1) node attribute transformation
(2) metapath-based subgraph generation
(3) node aggregation
(4) subgraph aggregation
HMSG의 전체적인 개요는 다음과 같습니다.
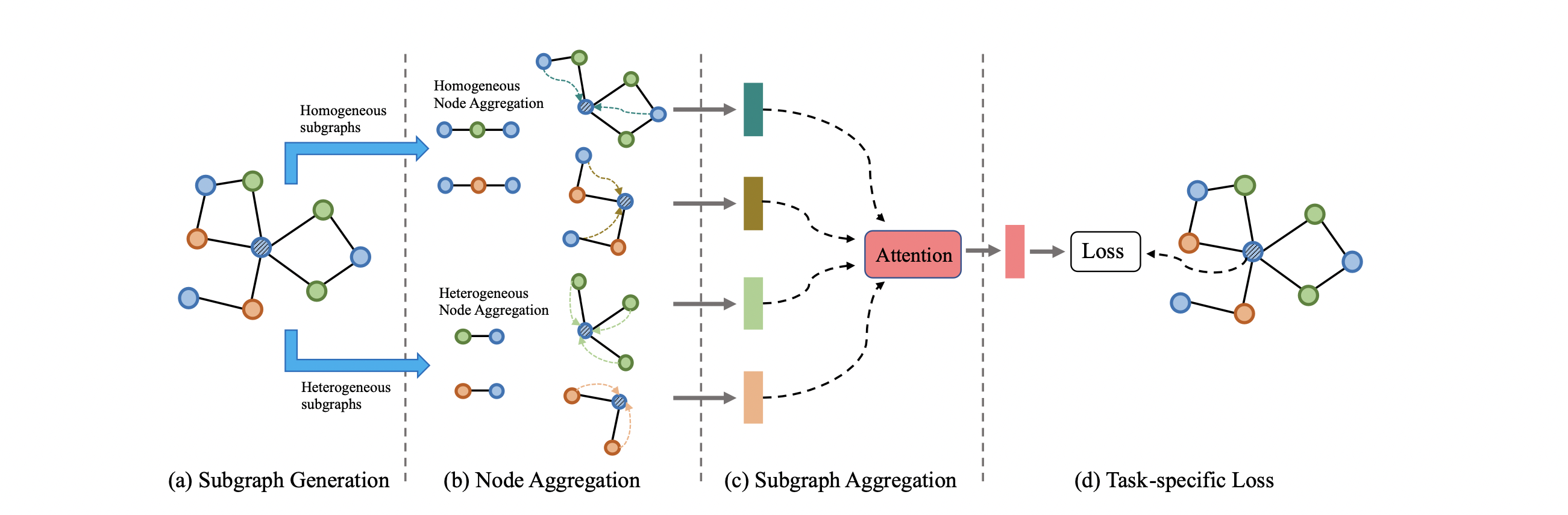
4.1 Node Attribute Transformation
첫 번째 파트는 서로 다른 타입의 노드 속성을 동일한 latent space로 투영(project)하여 attribute 정보를 전송할 수 있도록 하는 것이 목표입니다.
heterogeneous graph에서 다른 타입의 노드들은 다른 속성으로 구성되어 있습니다.
예를 들어 paper node는 Keywords, abstracts 같은 속성이 있을 것이고, author node는 연구 분야 같은 속성을 가지고 있겠죠.
이러한 속성들은 대체로 다른 feature space로 표현됩니다.
그러므로 노드의 각 타입에 따라 linear transformation metrix를 설계하여 동일한 latent space로 투영할 수 있게 해야 합니다.
타입 A의 특성을 가지고 있는 노드 $v \in V_A$가 있고,
$h_v^A$는 original feature vector를
$W_A$라는 node type A의 linear transformation matrix를 통해
$h'_v$는 노드 v의 projected feature vector로 변형할 수 있습니다.
$$ h'_v = W_A \cdot h^A_v$$
이러한 속성의 변환을 통해 서로 다른 유형의 노드 사이에 heterogenity한 특성 문제를 해결할 수 있으며, 그래프 내에 노드 사이의 정보 전송 및 수집을 강화할 수 있습니다.
4.2 Metapath-based Subgraph Generation
다른 metapaths는 다른 의미를 나타냅니다.
metapath의 시작 / 끝노드 타입에 따라서 두 가지 타입으로 나눌 수 있습니다. (Definition 4)
$$P = P^t, t \in {ho, he}$$
$ho$ : 시작과 끝 노드의 타입이 동일한 metapath
$he$ : 시작과 끝 노드가 서로 다른 타입인 metapath
각 metapath의 정보를 완벽하게 학습하기 위해서 위와 같이 서브그래프를 생성했고 , 각 서브그래프에 aggregation methods를 적용했습니다.
metapaths의 t 타입에 대해 생성된 서프그래프는 homogeneous subgraph $G^{ho}$와 heterogeneous subgraph $g^{he}$로 나누어질 수 있습니다.
$$g^t = g^{ho} \cup g^{he}$$
특정 타입의 노드에 대해서 서로 다른 서브그래프에서 이웃에 대한 연결은 다른 의미적 정보를 전달하므로 각 서브그래프는 특정 의미적 정보를 가진 상호작용 그래프로 간주할 수 있습니다. (?)
서브그래프들은 독립적이므로 learning tasks는 각 서브그래프에 대해 병렬적으로 수행될 수 있으며 이는 보다 효율적으로 학습할 수 있게 도와줍니다.
또한 homogeneous와 heterogeneous 서브그래프를 독립적으로 학습함으로써 유용한 정보들을 최대한 유지할 수 있게 됩니다.
4.3 Node Aggregation
이 단계에서는 각 서브그래프의 정보를 노드 간에 전송하는 일을 합니다.
homogeneous graph를 학습할 때는 GCN이나 GAT와 같이 우수한 연구가 이미 존재합니다.
각 heterogeneous subgraph는 서브그래프 내에 두가지 타입의 노드만이 존재하고, 서로 다른 유형의 노드 쌍 사이에만 연결이 존재하기 때문에 bipartite 형태의 그래프라고 볼 수 있습니다.
bipartite graph를 aggregation할 때는 heterogeneous graph의 1차 이웃의 정보가 주된 문제였습니다.
2차 이웃들, 즉 homogeneous 이웃들의 정보는 homogeneous graph aggregation을 통해서 얻을 수가 있기 때문입니다.
본 논문에서는 GraphSAGE 논문으로부터 영감받아 3가지 aggregators 후보를 제시합니다.
1) Mean
heterogeneous 이웃 노드들의 요소 별 featres를 평균내어 타겟 노드의 feature로 사용하는 것
$$ z_v = MEAN({h'_u, \forall u \in N_v}) $$
** $N_v$는 node v의 이웃들을 의미 **
2) Pooling
pooling 연산은 heterogeneous 이웃들에 대해 아래와 같은 방식으로 aggregate 합니다.
$$ z_v = max(\sigma (W_{pool}h'_u + b_{pool}), \forall u \in N_v) $$
$\sigma$는 non-linearity activation function을 의미하며, 본 논문에서는 ReLU 사용을 했다고 합니다.
$max$연산은 element-wise maximize 연산을 의미합니다.
$W_{pool}$과 $b_{pool}$은 learnable parameters입니다.
3) Attention
Self-attention mechanism은 효과적인 정보 aggregator라는 것은 이미 입증되었습니다.
서로 다른 이웃들은 타겟 노드에게 서로 다른 영향을 미칠 것이기 때문에 본 논문에서는 attention을 각 이웃의 중요도를 학습하는데 사용합니다
또한 homogeneous와 heterogeneous 그래프로부터 정보를 수집하는데에도 self-attention mechanism을 사용합니다.
node type $A$로부터 시작되는 metapath $P_A^t$에 의해 생성 된 그래프 $G$가 있다고 가정합시다.
타겟 노드가 $v$이고, 그래프 $G$의 node pair $(v, u)$가 주어졌을 때, graph attention layer를 통해 node $u$가 타겟 노드 $v$에게 얼마나 기여하는지를 측정하는 중요도 $e_{vu}^G$를 학습합니다.
homogeneous subgraph에서 노드 $u$의 중요도는 아래와 같이 공식화할 수 있습니다.
$$e_{vu}^G = LeakyReLU(a^T_G \cdot [h'_v || h'_u])$$
반면에 heterogeneous subgraph에서 노드 $u$의 중요도는 아래와 같습니다.
$$e_{vu}^G = LeakyReLU(a^T_G \cdot h'_u)$$
참고로 || 는 concatenate 연산자입니다!
이런식으로 노드 $u \in N^G_v$에 대한 $e_{vu}^G$를 구할 수 있습니다.
$N^G_v$는 그래프 $G$에 있는 노드 $v$에 직접적으로 연결 된 neighbors를 의미합니다.
여기에 softmaxf 함수를 덧붙여 normalized weight cofficient $\alpha^G_{vu}$를 구할 수 있습니다.
$$\alpha^G_{vu} = softmax(e^G_{vu}) = \frac{exp(e^G_{vu})} {\Sigma _{k \in N^G_v } exp(e^G_{vk})}$$
마지막으로, 서브그래프 $G$ 내의 node $v$의 임베딩은 아래의 coefficients로 표현이 됩니다.
이는 이웃들의 projected features를 aggregated하여 얻을 수 있습니다.
$$z_v^G = \sigma (\Sigma _{u \in N^G_v} \alpha ^G_{vu} \cdot h'_u)$$
$z_v^G$는 서브그래프 $G$의 노드 $v$에 대한 outputdlrh, $\sigma$는 activation function입니다.
그래프의 heterogeneity에 의한 variance를 줄이기 위해, 그리고 학습을 조금 더 안정적으로 진행하기 위해서 self-attention을 multiple heads로 확장했습니다.
특히, 독립적인 attention mechanisms을 K번 반복하고 학습 된 임베딩을 연결짓는 방식을 사용했습니다.
$$z_v^G = \parallel_{k=1}^K \sigma(\Sigma _{u \in N_v^G} \alpha_{vu}^G \cdot h'_u)$$
요약하자면, node type이 $A$인 metapath-based graphs $g^t_A = {G_1, ..., G_x}$와 projected node features $h'$가 주어졌을 때 타겟 노드의 group of embeddings ${z_v^{G_1}, ..., z_v^{G_x}}$가 Figure 2.(b)처럼 생성이 되는 것입니다.
4.4 Subgraph Aggregation
노드 aggregation 단계를 통해 서로 다른 서브그래프 내의 각 노드의 임베딩을 얻을 수 있습니다.
더 많은 의미적 정보를 얻기 위해서 attention mechanism을 사용하여 서로 다른 서브그래프에 서로 다른 weights(중요도에 따라)을 적용합니다.
먼저, node aggregation으로부터 얻은 임베딩은 nonlinear transformation을 통해 변환합니다.
그러 ㄴ다음 각 서브 그래프 $G_i \in g_A$내의 모든 노드 임베딩을 평균내어 다 더해줍니다.
$$w_{G_i} = \frac {1} {|V_A|} \Sigma _{v \in V_A} q^T_A \cdot tanh (M_A \cdot z_v^{G_i} + b_A)$$
** $q_A$는 node type A에 대한 parameterized attention vector이고, $M_A$와 $b_A$는 leanable parameters입니다.
서로 다른 subgraphs $G_i$에서 coefficients를 쉽게 비교하기 위해 softmax function을 사용하여 coefficients를 normalize하고, 모든 서브그래프의 가중치를 더했습니다.
$$ \beta_{G_i} = \frac exp(w_{G_i}) {\Sigma _{k=1}^{|G_A|} exp(w_{G_k})}$$
$$z_v^{G_A} = \Sigma _{i=1}^{|G_A|} \beta_{G_i} \cdot z_v^{G_i}$$
이 단계에서 모든 노드에 대한 최종 임베딩을 구할 수 있고, 이는 Figure 2(c)에 해당하는 부분입니다.
4.5 Training
4.1 ~ 4.4를 통해 각 노드의 node representations를 얻을 수 있습니다.
어떤 tasks를 위해 사용하느냐에 따라 다른 Loss function을 사용할 수 있습니다.
HMSG의 학습 패러다임은 크게 semi-supervised learning과 unsupervised learning으로 나누어집니다.
1) semi-supervised learning
그래프 내의 매우 적은 양의 노드만이 label information을 가지고 있습니다.
이 경우 cross entropy를 사용하며 학습 및 최적화를 진행한다고 합니다.
$$ L = - \Sigma _{v\inV_L} y_v log y'_v$$
여기서 $V_L$은 labeled nodes이며 $y_v$와 $y'_v$는 ground truth 및 노드 v의 predicted probability vector입니다.
2) Unsupervised learning
label information이 아예 보이지 않는 경우입니다.
이럴 경우 negative sampling을 통해 아래의 새롭게 만들어진 Loss function을 최소화함으로써 모델의 가중치를 최적화할 수 있습니다.
$$ L = - \Sigma _{(v, u) \in V^+} log \sigma (h_v^T \cdot h_u) - \Sigma _{(v, u') \in V^-} log \sigma(-h_v^T \cdot h_{u'})$$
여기서 $V^+$는 연결된 node 쌍 (positive)를 의미하며, $V^-$는 모든 연결되지 않은 노드 쌍으로부터 랜덤하게 샘플링 된 (negative) 것을 의미합니다.
전체적인 HMSG의 알고리즘은 아래와 같습니다.

'DL & ML > Graph' 카테고리의 다른 글
| [DGL] remove_edges로 그래프 내 특정 edge 제거하기 (0) | 2022.03.07 |
|---|---|
| [DGL] RelGraphConv에서 IndexError: index out of range in self 문제! (0) | 2022.03.07 |
| [DGL] heterogeneous graph를 homogeneous graph로 변환할 때 edata, ndata 함께 전달하기 (0) | 2022.03.07 |
| [DGL] TypeError : default_collate 에러 (DGL.batch, collate_fn) (0) | 2022.03.03 |
| [DGL] 기본 message passing layer 만들기 (0) | 2022.02.04 |
